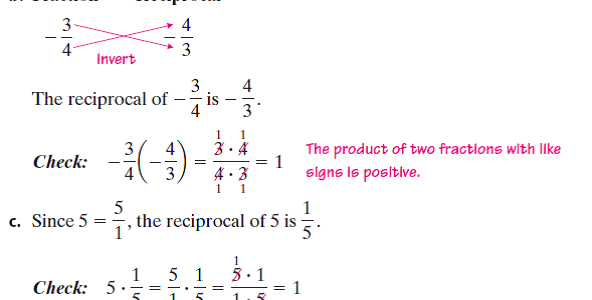This guide will teach you more about methods to use reciprocals and how to evaluate reciprocals.
In mathematics, reciprocals are widely used in infractions, numbers, multiplicative inverse, and many other branches of math. Reciprocal provides the easiest ways to solve the fractions, especially it is useful in the division of two fractions.
What Are reciprocals?
A pair of numbers whose product gives result one or gives an output one is said to be reciprocal. Reciprocal is also known as multiplicative inverse. Whenever a number is given in a fraction the way of finding the reciprocal is very simple as you have to change the places of numerator and denominator. In mathematics, each number has an inverse, that inverse is said to be reciprocal. In simple words, when we take the product of a number along with its inverse the output must be one.
For example, we have a number such as 7 then the inverse of 7 is 1/7, and the product of 7 and its inverse is one such as 7 x 1/7 = 1.
Reciprocal provides the easiest way to calculate the division of two fractions.
For example, 2/3 / 2/6 we will reciprocate the last term in order to convert the division into multiplication such as,
2/3 x 6/2 = 2
We can also use reciprocal for the division of a number and a fraction.
For example, 3 / (1/3) = 3 x 3/1 = 3 x 3 = 9
Methods to use reciprocals
There are various methods to use reciprocals.
1. Reciprocal of a decimal number
We can find the decimal number using a reciprocal calculator. To calculate the reciprocal of a decimal number manually, just place that number in the denominator of 1.
0.x = 1/0.x or 0.x-1
Example 1
Find the reciprocal of 0.6?
Solution
Step 1: Write the number.
0.6
Step 2: Place the given number in the denominator of 1.
1/0.6 = 10/6 = 5/3
Thus, the reciprocal of 0.6 is 5/3. Which can also be written as 1.6667
Example 2
Find the reciprocal of 11.5?
Solution
Step 1: Write the number.
11.5
Step 2: Place the given number in the denominator of 1.
1/11.5 = 10/115 = 2/23
Thus, the reciprocal of 11.5 is 2/23. Which can also be written as 0.087.
2. Reciprocal of a number
We can find the reciprocal of a single number. To calculate the reciprocal of a single number just place that number in the denominator of 1.
x = 1/x or x-1
Example 1
Find the reciprocal of 6?
Solution
Step 1: Write the number.
6
Step 2: Place the given number in the denominator of 1.
1/6
Thus, the reciprocal of 6 is 1/6. Which can also be written as 0.1667.
Example 2
Find the reciprocal of 115?
Solution
Step 1: Write the number.
115
Step 2: Place the given number in the denominator of 1.
1/115
Thus, the reciprocal of 115 is 1/115. Which can also be written as 0.087.
3. Reciprocal of a fraction
We can find the reciprocal of a fraction. To calculate the reciprocal of a fraction we have to change the places of numerator and denominator. As take the value of the numerator in the place of the denominator and the value of the denominator in place of the numerator.
Example 1
Find the reciprocal of 7/6?
Solution
Step 1: Write the fraction.
7/6
Step 2: Change the places of numerator and denominator.
6/7
Thus, the reciprocal of 7/6 is 6/7. Which can also be written as 0.8571
Example 2
Find the reciprocal of 17/68?
Solution
Step 1: Write the fraction.
17/68
Step 2: Change the places of numerator and denominator.
68/17
Thus, the reciprocal of 17/68 is 68/17. Which can also be written as 4.
4. Reciprocal of a mixed fraction
We can find the reciprocal of a mixed fraction. To calculate the reciprocal of a mixed fraction, first, we have to change the mixed fraction into a simple fraction and then change the places of numerator and denominator. As take the value of the numerator in the place of the denominator and the value of the denominator in place of the numerator.
Example 1
Find the reciprocal of 1 7/6?
Solution
Step 1: Write the fraction.
1 7/6
Step 2: Convert the mixed fraction to improper fraction.
1 7/6 = (6 x 1 + 7)/6 = 13/6
Step 3: Change the places of numerator and denominator.
6/13
Thus, the reciprocal of 1 7/6 is 6/13. Which can also be written as 2.1667.
Example 2
Find the reciprocal of 2 17/68?
Solution
Step 1: Write the fraction.
2 17/68
Step 2: Convert the mixed fraction into a simple fraction.
2 17/68 = (68 x 2 + 17)/68 = 153/68
Step 2: Change the places of numerator and denominator.
68/153
Thus, the reciprocal of 2 17/68 is 68/153. Which can also be written as 2.25.
How To Evaluate Reciprocals
Here are some examples to understand the concept of reciprocal and how to evaluate reciprocals
Example 1
Find the division of 36/14 and 6/7?
Solution
Step 1: Write the fractions along with a division sign among them.
36/14 / 6/7
Step 2: Reciprocate the last term in order to convert the division sign into a multiplication sign.
36/14 x 7/6
Step 3: solve.
36/14 x 7/6 = 6/2 = 3
Example 2
Find the division of 16/14 and 4/7?
Solution
Step 1: Write the fractions along with a division sign among them.
16/14 / 4/7
Step 2: Reciprocate the last term in order to convert the division sign into a multiplication sign.
16/14 x 7/4
Step 3: solve.
16/14 x 7/4 = 4/2 = 2
Example 3
If 16/5 is a number x is 80. Find the value of x?
Solution
Step 1: write mathematical form.
16/5 x = 80
Step 2: we need the value of x, take the coefficient of x to the other side of the equality sign.
x = 80 / 16/5
Step 3: Reciprocate the last term of the right-hand side in order to convert the division sign into a multiplication sign.
x = 80 x 5/16 = 5 x 5 = 25
- Read Also: Difference Between HND and BSC
Conclusion: How To Evaluate Reciprocals
A pair of numbers whose product gives result one or gives an output one is said to be reciprocal. We can use reciprocal for numbers, decimals, fractions, and mixed fractions. Reciprocal make our work easier. We can apply reciprocal on the division of two fractions which convert the last value and change the division sign into a multiplication sign.
- CAC Accredited Agent Registration 2025: Online Requirements - January 15, 2024
- Best Coding Schools in Lagos 2025 - October 23, 2023
- How AI Technology Plays a Role in Education & Business - August 25, 2023